Rychlost světla je předmětem částicové i jaderné fyziky. Vědci byla po několika desetiletí zpřesněna a upravena na c = 299 792 458 m/s ve vaku. První historický milník měření uskutečnil na počátku 17. století Italský astronom Galileo Galilei, jenž měřením prokázal, že velikost rychlosti světla je větší než zvuku a je konečná. K experimentu potřeboval asistenta, který se postavil na druhý kopec vzdálený 1.6 km od prvního, kde stál Galileo. K výsledku se dopracoval pomocí vzorce c = d / (t2 – t1) , kde c je označení latinského slova celeritas (rychlost) a d je vzdálenost obou kopců. V čase t1 Galileo odkryl lucernu a poté signál přijal asistent, kdy v čase t2 taktéž odkryl lucernu. Koncept byl zatížen několika nepřesnostmi a problémy včetně tehdejšího technické vybavení a malé vzdálenosti obou pozorovatelů. Galileiho metoda byla ověřena až misí Apollo umístěním koutového odražeče na povrch Měsíce, na který byl směřován laser ze Země. Galileo je pouhý zlomek z této historie. Ani v tomto článku nejsou uvedeni všichni, ale jenom důležitá většina.
Autor: Model (Stručnější historie času).
Römerův odhad
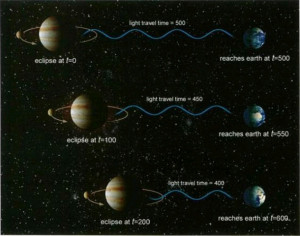
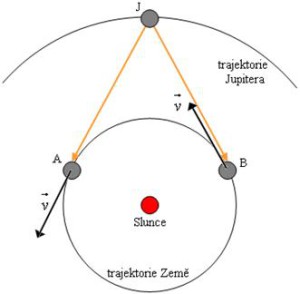
Přesný objev přinesl známý dánský astronom Ole Christensen Römer, když v roce 1676 demonstroval svá měření na nejvnitřnějším měsíci Io planety Jupiter v Kodani. V poloze nejblíž Jupiteru změřil časový interval zákrytu měsíce Io. Ze svých pozorování zjistil, že naměřená perioda se od skutečné hodnoty nejvíce liší právě ve chvíli, kdy je planeta v kvadratuře (viz obr.) Z těchto informací odvodil rychlost světla cca 220 000 km/s.
t1 ( c – v ) = t2 ( c + v ), kde t1 je časový interval zákrytu Io v poloze A, t2 v poloze B, …rychlost světla ve vaku dostaneme vzorcem c = (t1 + t2) / (t1 – t2) v a rychlost Země v = 29,783 km/s.
Autor: businessinsider.com
Bradleyova měření
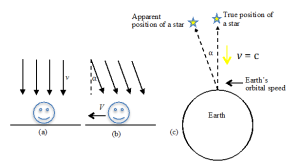
Další měření odvodil z aberace hvězd (tj. odhylkou hvězd v důsledku odchylky světelného paprsku od původního směru k tělesu v důsledku skládání rychlosti světla a rychlosti Země) známý astronom James Bradley. Kromě rychlosti Země musel znát tangens úhlu α (aberace hvězd) pro který platí:tg α = v sin (β) / c, kde β je úhel sevřený směry k hvězdě a k bodu na obloze ke kterému směřuje, nazývanému apex.
Autor: hamamatsu.com
Další (ne)astronomický experiment se uskutečnil až roku 1849. Později se měření zpřesňuje a přichází se na nové metody jak je určit.
Ozubené kolo
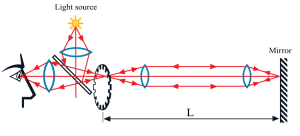
Autor: hamamatsu.com
Kolo mělo několik set zubů a frekvenci otáčení 100/s. 8 km před kolem stálo zrcátko a za kolem zdroj světla. Jakmile světelný paprsek dopadající na polopropustné zrcadlo byl přerušován zuby kola. V některých okamžicích prošel paprsek mezi zuby a dopadl na zrcadlo, které je odrazilo do oka pozorovatele. Tímto získal až interesantní výsledek: 301 000 km/s. Došel k tomu, že c = 4Lnf, L – vzdálenost mezi ozubeným kolem a odrážejícím zrcadlem postaveným před ním, n – počet zubů u kola, f – frekvence otáčení, přičemž vzdálenost L musela být větší než vzdálenost zdroje světla od pozorovatele.
Experimenty prováděl i ve vodě.
Jean Foucault
Později francouzský fyzik Foucault nahradil rotujícím zrcadlem ozubené kolo z předchozího experimentu. Nastavil úhel otáčení zrcadla ve směru hodinových ručiček v čase t0. Světelný paprsek byl od tohoto zrcadla odražen na pevné stojící zrcadlo o 18 m dál a zpátky dopadl na rotující, který za tuto dobu změnil úhel od okamžiku t0.
Autor: pas.rochester.edu
Úhlová rychlost otáčení zrcadla (omega) = 2 π f. c = 4ωL1 L2 / Δs, odkud Δs dopočítal Δs = 2Δ α L1. Výsledek: 298 000 km/s.
Později tento pokus využil A. A. Michelson a přesnějším měřením díky lepšímu vybavení a hlavně rotujícímu osmibokému hranolu se zrcadlícími stěnami určil velikost rychlosti světla na 299 909 km/s. V roce 1888 zasáhl do měření i Hertz, který ale pro změnu měřil velikost rychlosti radiových vln, ale dostal se k výsledku 300 000 km/s.
Pokusy prováděl i ve 20. století Michelson, který opět tato měření o kousek zpřesnil na 299 798 km/s. Dnes již umíme změřit a určit velikost rychlosti světla s přesností na metr za sekundu.